BITÁCORA 7, ENIGMÁTICA MATEMÁTICA

RAZÓN DORADA

La geometría es tan amplia y tan práctica que no deja de sorprender con sus secretos y enigmas así como con sus aplicaciones. Una de las maravillas que nos ofrece es la razón dorada o también conocida como número áureo, número dorado, razón áurea, media áurea, proporción áurea o divina proporción. Es la relación o proporción que guardan entre sí dos segmentos de rectas. Puede encontrarse no solo en figuras geométricas, sino también en la naturaleza.

El primero en hacer un estudio formal sobre el número áureo fue Euclides, unos tres siglos antes de Cristo, en su obra Los Elementos. Euclides definió su valor diciendo que  "una línea recta está dividida en el extremo y su proporcional cuando la línea entera es al segmento mayor como el mayor es al menor." En otras palabras, dos números positivos a y b están en razón áurea si y sólo si (a+b) / a = a / b. El valor de esta relación es un número que, como también demostró Euclides, no puede ser descrito como la razón de dos números enteros (es decir, es irracional y posee infinitos decimales) cuyo su valor aproximado es 1,6180339887498..., dicho número está representado por la letra griega φ (fi), en honor al escultor griego Fidias.

Casi 2000 años más tarde, en 1525, Alberto Durero publicó su “Instrucción sobre la medida con regla y compás de figuras planas y sólidas”, en la que describe cómo trazar con regla y compás la espiral basada en la sección áurea, la misma que hoy conocemos como “espiral de Durero”. Casi todas las espirales que aparecen en la naturaleza, como en el caso del girasol o las piñas de los pinos poseen esta relación áurea.

                     

Leonardo Fibonacci, descubrió la serie que nos lleva a phi. En el siglo XII, Leonardo Fibonacci descubrió una serie numérica simple que es la base de la increíble relación que encontramos detrás de phi. Empezando con 0 y 1, cada número de la serie es simplemente la suma de los dos anteriores. Por lo tanto, la serie queda construida de la siguiente manera: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .

La razón (proporción) de cada par sucesivo de números en la serie se aproxima a phi (1.618...). Así es como si dividimos 5 entre 3 obtenemos 1.666..., y 8 entre 5 da 1.60. En la medida en la que vayamos más lejos del 0 (punto de inicio de la secuencia), más nos acercamos al valor de phi.

El primer uso conocido del adjetivo áureo, dorado, o de oro, para referirse a este número lo hace el matemático alemán Martin Ohm, hermano del célebre físico Georg Simon Ohm, en la segunda edición de 1835 de su libro Die Reine Elementar Matematik (Las Matemáticas Puras Elementales).

¿Por qué es tan importante éste valor matemático? Posee muchas propiedades interesantes y aparece, escondido y enigmático, en los sitios más dispares dándole un carácter estético especial a los objetos que contienen este número, es posible encontrar esta relación en diversas obras de la arquitectura y el arte. Por ejemplo, el Hombre de Vitruvio, dibujado por Leonardo Da Vinci y considerado un ideal de belleza, está proporcionado según el número áureo. También el rostro de la Mona Lisa encierra un “rectángulo dorado” perfecto. Obviamente, Leonardo no fue el único en utilizar esta proporción en su obra. Miguel Ángel, por ejemplo, hizo uso del número áureo en la impresionante escultura El David, desde la posición del ombligo con respecto a la altura, hasta la colocación de las articulaciones de los dedos. La proporción aurea se encuentra en las espirales del interior de los caracoles. En la arquitectura la relación entre las partes, el techo y las columnas del Partenón de Atenas, por ejemplo, también se relacionan mediante el número áureo. Muchos productos de consumo masivo se diseñan siguiendo esta relación, ya que resultan más agradables o cómodos. Las tarjetas de crédito o las cajas de cigarrillos poseen dimensiones que mantienen esta proporción. El número áureo puede encontrarse por todas partes, y a menudo ni siquiera somos consientes de que está allí. Pero en general, cuando algo nos resulta atractivo, esconde entre sus partes esta relación. ¿No es asombroso?

¿Cómo podemos notar de manera sencilla esta maravilla matemática y la belleza en todo lo que nos rodea?

En esta nueva sesión de geometría aprendí algo inusual: la belleza se puede medir. Y para poder hacerlo es necesario realizar un instrumento de medición, un compás dorado. Pa ello es necesario seguir el proceso de construcción:

1.    Traza un segmento de recta AB

2.    Encuentra el punto medio del segmento (C).

3.    Traza una perpendicular a la recta AB, a partir del punto B.

4.    Haciendo centro en el punto medio de este segmento (C) y tomando como extremo B traza un circulo con radio CB que corte a la perpendicular en el punto D.

5.    Une los puntos AD mediante un segmento, éste será la hipotenusa del triángulo rectángulo.

6.    El punto donde la hipotenusa o segmento AD corta la circunferencia, se nombra E.

7.    Haciendo centro en A y como extremo E, traza una segunda circunferencia de radio AE.

8.    El punto donde ésta segunda circunferencia corta al segmento AB, se nombra F, y es el punto que buscamos para realizar nuestro compás.

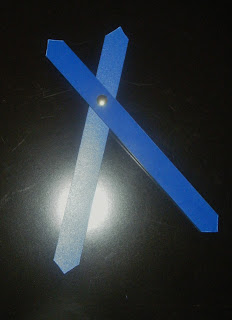
9.    Una vez encontrado ese punto trazamos dos segmentos AB en una superficie resistente, puede ser plástico o cartón grueso y ubicamos el punto F en ellos para unir los dos segmentos mediante una chincheta, así es como terminamos nuestro compás y podemos utilizarlo para saber si un objeto tiene la razón dorada.

                  

Observemos entonces cómo se da la proporcionalidad de los objetos.
                                     

Al medir el lado más grande del celular y compararlo con el lado menor observamos que la abertura del compás no cambia, se mantiene, cumpliendo así con la proporción dorada.

Esto, como ya dijimos tambien ocurre en la arquitectuta.

                          

                                

                                 

                         

 

                            

Las figuras que están “proporcionadas” según el número áureo nos resultan más agradables. Aunque recientes investigaciones revelan que no hay ninguna prueba que conecte esta proporción con la estética griega, lo cierto es que a lo largo de la historia se ha utilizado para “embellecer” muchas obras.


http://es.wikipedia.org/wiki/N%C3%BAmero_%C3%A1ureo
http://www.psicogeometria.com/matematica.html
http://www.neoteo.com/numero-aureo-belleza-matematica

LA CIRCUNFERENCIA, SUS RECTAS, SEGMENTOS Y ÁNGULOS

NOTA: Da clic a los enlaces de color rojo para observar los elementos de la circunferencia.

LA CIRCUNFERENCIA

Es una línea curva cerrada y plana formada por un conjunto de puntos que equidistan de otro punto fijo llamado centro “O”, la distancia constante del centro a todos los puntos de la circunferencia recibe el nombre de radio.

También podemos definirá a la circunferencia como el contorno o perímetro del círculo.

PUNTOS, SEGMENTOS Y RECTAS DE LA CIRCUNFERENCIA

·      Centro, el punto interior equidistante de todos los puntos de la circunferencia.

·      Radio, el segmento que une el centro con un punto cualquiera de la circunferencia.

·      Diámetro, el mayor segmento que une dos puntos de la circunferencia y  que necesariamente pasa por el centro.

·      Cuerda, el segmento que une dos puntos de la circunferencia; (las cuerdas de longitud máxima son los diámetros).

·      Arco, el segmento curvilíneo de puntos pertenecientes a la circunferencia.

·     Semicircunferencia, cada uno de los dos arcos delimitados por los extremos de un diámetro.

En el plano, una recta puede intersecar a una circunferencia en un punto, intersecarla en dos puntos o no intersecarla.

·           Las rectas que intersecan a la circunferencia en un solo punto se llaman rectas tangentes a la circunferencia. Al punto en el que la tangente interseca a la circunferencia se llama punto de tangencia; una recta tangente a una circunferencia es perpendicular al radio que une el punto de tangencia con el centro, por lo cual, la distancia que hay del centro a la recta tangente es igual al radio.

·           Las rectas que intersecan en dos puntos a la circunferencia se llaman rectas secantes. La distancia del centro de la circunferencia a la recta secante es menor que el radio.

·           Las rectas que no intersecan a la circunferencia se llaman rectas exteriores. La distancia del centro de la circunferencia a la recta exterior es mayor que el radio.

ÁNGULOS EN LA CIRCUNFERENCIA

·            Ángulo central tiene su vértice en el centro por lo que sus lados contienen a dos radios. La amplitud de un ángulo central es igual a la del arco que abarca.

·            Ángulo inscrito su vértice es un punto de la circunferencia y sus lados son dos cuerdas.

·            Ángulo semi-inscrito su vértice es un punto de la circunferencia y sus lados contienen una cuerda y una recta tangente a la circunferencia. El vértice es el punto de tangencia. La amplitud de un ángulo semi-inscrito es la mitad de la del arco que abarca.

·            Ángulo interior su vértice está en el interior de la circunferencia. La amplitud de un ángulo interior es la mitad de la suma de dos medidas: la del arco que abarcan sus lados más la del arco que abarcan sus prolongaciones.

·            Ángulo exterior tiene su vértice en el exterior de la circunferencia  y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella.

TEOREMAS DE LOS ÁNGULOS EN LA CIRCUNFERENCIA

TEOREMA DEL ÁNGULO CENTRAL: La medida de un arco es la de su ángulo central correspondiente o viceversa.  

  

   AOB = AB

TEOREMA DEL ÁNGULO INSCRITO: Mide la mitad del arco que abarca.

AOB = ½ AB

Un ángulo inscrito y uno central cumplen con la siguiente relación: “la medida de un ángulo inscrito es la mitad de la medida del ángulo central que subtiende el mismo arco”.

TEOREMA DEL ÁNGULO SEMI-INSCRITO: Mide la mitad del arco que abarca.

AOB = ½ AB

TEOREMA DEL ÁNGULO INTERIOR: Mide la mitad de la suma de las medidas de los arcos que abarcan sus lados y las prolongaciones de sus lados.

AOB = ½ (AB + CD)

TEOREMA DEL ÁNGULO EXTERIOR: Mide la mitad de la diferencia entre las medidas de los arcos que abarcan sus lados sobre la circunferencia.

AOB = ½  (AB - CD)

http://www.matematica.raimapu.cl/guias/2medio/circunferencia/guia1.pdf

http://es.scribd.com/doc/20457620/Circunferencia-teoremas

http://www.educared.org/wikiEducared/%C3%81ngulos_en_las_circunferencias.html

BITÁCORA SEIS, DONALD EN EL PAÍS DE LAS MATEMÁTICAS

Nunca pensé que una película infantil nos pudiera enseñar tanto de matemáticas de manera sencilla pero a la vez tan interesante, llevándonos a explorar y a descubrir que las matemáticas están presentes en todo lo que nos rodea.

En mi opinión a pesar de que en la película se manejan conceptos quizá un poquito elevados para un niño, si es una película apta para infantes y también para adolescentes, jóvenes y adultos. Me agrado mucho y me pareció excelente la manera de introducirnos hacia conceptos matemáticos como Pitágoras, los pitagóricos y la música, el número de oro, el rectángulo áureo en la naturaleza, las matemáticas en los juegos y la idea del infinito en la imaginación.

En este cortometraje es fácil darse cuenta de la utilidad de las matemáticas, pues históricamente la película nos lleva hasta Grecia para mostrarnos que la música y las matemáticas están íntimamente ligadas, que la proporción aurea la encontramos en la naturaleza que nos rodea. Además también podemos notar que la aplicación de esta disciplina se ha dado en la arquitectura, el arte, los deportes y juegos de mesa, y todo ello nos lleva finalmente a reflexionar acerca de que la imaginación no tiene límites y en ella podemos crear matemáticas y conocimientos que nos servirán para abrir nuevas puertas del conocimiento que aún permanecen cerradas. Para finalizar no me queda más que decir que sigamos disfrutando y descubriendo ese mundo de las matemáticas y que veamos cada vez más claramente la utilidad de éstas en nuestra vida y todo lo que podemos lograr a través de ellas. La película nos invita a aprender que las matemáticas no son exclusivas de “locos” o matemáticos propiamente dicho, sino que absolutamente todos podemos abrir esas maravillosas puertas del conocimiento.

BITÁCORA 5, CALIDOCICLO

 Al iniciar esta nueva sesión me preguntaba qué era un calidociclo, nunca creí que me quedaría tan sorprendida al finalizar el trazado y su construcción. Al indagar un poco comprendí por qué es tan fascinante.

La palabra calidociclo o caleidociclo proviene del griego kalos (bellos), eîdos (figuras) y kîklos (anillo). Es un anillo geométrico tridimensional, articulado por pirámides unidas por sus aristas. Pueden giran sobre sí mismos indefinidamente sin romperse ni deformarse en torno a su centro. Al principio se me complico su elaboración, pero ya después en una segunda construcción me pareció muy sencilla debido a la práctica.

Los calidociclos son figuras geométricas dignas de admirarse puesto que nos permiten desarrollar la creatividad, la imaginación y la sensibilidad geométrica; estas figuras son una muestra más de que la geometría puede está presente en diferentes ámbitos de la vida cotidiana y que podemos servirnos de ella, como por ejemplo en el diseño gráfico, la mercadotecnia o publicidad, como material didáctico, de composición y diseño gráfico, industrial o arquitectónico, así como en el arte.

Cabe señalar que los Caleidociclos forman parte de una disciplina que se llama Arquitectura de papel y que los ejemplos más conocidos de calidociclos son los que están formados por tetraedros.

http://www.grupoalquerque.es/ferias/2010/archivos/pdf/caleidociclo.pdf

SÓLIDOS PLATÓNICOS

Un sólido es un poliedro (en griego, polys, "múltiples"; hedra, "cara"), es decir, una figura tridimensional conformada por varias caras planas de diversas formas (polígonos).

Los sólidos platónicos, son poliedros, cuyas caras son polígonos regulares iguales entre sí,  y en cuyos vértices se unen el mismo número de caras. Así pues, se dice por definición que un sólido platónico es un poliedro regular. La regularidad quiere decir que todas las caras y vértices del poliedro regular son iguales entre sí.

Los sólidos platónicos son cinco poliedros: el tetraedro, cubo, octaedro, dodecaedro e icosaedro. Los prefijos Tetra, Hexa, Octa, Dodeca e Icosa indican el número de polígonos (caras) que forman el cuerpo:

ü  Tetraedro regular (4 vértices, 6 aristas, 4 triángulos equiláteros como caras).

ü  Hexaedro regular o cubo (8 vértices, 12 aristas, 6 cuadrados como caras).

ü  Octaedro regular (6 vértices, 12 aristas, 8 triángulos equiláteros como caras).

ü  Dodecaedro regular (20 vértices, 30 aristas, 12 pentágonos como caras).

ü  Icosaedro regular (12 vértices, 30 aristas, 20 triángulos equiláteros como caras).

El origen de los sólidos platónicos se encuentra en la antigua Grecia; sin embargo la primera referencia que se conoce sobre estos poliedros, proviene de un yacimiento neolítico en Escocia, donde se encontraron figuras de barro de aproximadamente 2000 a.C. Se cree que se trataba de elementos decorativos o, tal vez, de algún tipo de juego.

El nombre de sólido platónico es en honor al filósofo griego Platón, a quien se atribuye haberlos estudiado en primera instancia, pero también se conocen como cuerpos cósmicos, sólidos pitagóricos, sólidos perfectos, poliedros de Platón o, con más precisión, poliedros regulares convexos ya que fueron estudiados y descriptos por otros geómetras y matemáticos griegos, Euclides, Pitágoras y otros, que los consideraban perfectos e interesantes.

Los pitagóricos los concibieron como figuras místicas que contienen la clave para entender el universo. Por otra parte se cree que fue Empédocles el primero que asoció el cubo, el tetraedro, el icosaedro y el octaedro con la tierra, el fuego, el agua y el aire, respectivamente. Estas sustancias eran los cuatro "elementos" de los griegos antiguos. Luego Platón asoció el dodecaedro con el Universo pensando que, dado que era tan distinto de los restantes (por sus caras pentagonales) debía tener relación con la sustancia de la cual estaban hechos los planetas y las estrellas, (se creía que los cuerpos celestes debían estar hechos de un elemento distinto del que estaban hechas las cosas que rodean al hombre en la Tierra).

Platón, en su obra Timaeus, asoció cada uno de los cuatro elementos que según los griegos formaban el Universo: “El fuego está formado por tetraedros; el aire, de octaedros; el agua, de icosaedros; la tierra de cubos; y como aún es posible una quinta forma, Dios ha utilizado ésta, el dodecaedro pentagonal, para que sirva de límite al mundo”. Por este motivo estos poliedros reciben el nombre de sólidos platónicos. Sin embargo, quién verdaderamente formaliza, y consagra los sólidos platónicos como elementos matemáticos y realiza construcciones de los mismos, inscribiéndolos en la esfera, es Euclides de Alejandría, quien en su libro los Elementos demuestra un total entendimiento de las figuras. Así pues, los sólidos platónicos quedan introducidos en el mundo de las matemáticas de forma definitiva.

Nos preguntaremos ¿Por qué hay sólo 5 sólidos platónicos?  La respuesta, porque es imposible construir otro sólido diferente de los anteriores que cumpla todas las propiedades exigidas, es decir, convexidad y regularidad. Para mostrar por qué son cinco, y no más, se suele deducir del modo siguiente:

ü  Cada vértice debe ser común por lo menos a tres caras para que se forme un sólido. (Si fuera común a dos, las caras estarían pegadas y no tendríamos un sólido.)

ü  La suma de los ángulos interiores de las caras que se encuentran en cada vértice debe ser menor que 360°, de manera que la figura se cierre, que no sea plana.

ü  Dado que cada ángulo interior de un triángulo equilátero mide 60°, tomando en cuenta lo señalado en los dos puntos anteriores, en un vértice podrían concurrir tres, cuatro o cinco de ellos. Ésos son los casos del tetraedro, el octaedro y el icosaedro, respectivamente. Cada ángulo interior de un cuadrado mide 90°, de modo que sólo podemos hacer coincidir tres de ellos en cada vértice. Ése es el caso del cubo. Los ángulos interiores del pentágono regular miden 108°. Poniendo tres de ellos en cada vértice se obtiene un dodecaedro. Con los polígonos siguientes ya no es posible formar poliedros regulares: los ángulos interiores de un hexágono miden 120° y no es posible poner tres juntos sin llegar al límite de 360°; los ángulos interiores de los siguientes son aún mayores.

ü  Todas las caras de un sólido platónico son polígonos regulares iguales.

ü  En todos los vértices de un sólido platónico concurren el mismo número de caras y de vértices.

ü  Todas las aristas de un sólido platónico tienen la misma longitud.

ü  Todos los ángulos diedros que forman las caras de un sólido platónico entre sí son iguales.

ü  El Teorema de poliedros de Euler fija que el número de caras de un poliedro platónico más su número de vértices es siempre igual a su número de aristas más dos, es decir:

c + v = a + 2

http://www.luventicus.org/articulos/03Tr001/index.html

http://www.iessandoval.net/sandoval/aplica/activi_mate/actividades/poliedros/marco_poliedros.htm

http://es.wikipedia.org/wiki/S%C3%B3lidos_plat%C3%B3nicos